Lista Complementar
MATEMÁTICA BÁSICA

PALAVRAS PROPAROXÍTONAS

As palavras proparoxítonas são aquelas em que a antepenúltima sílaba é a tônica, ou seja, a sílaba que se pronuncia com maior intensidade. Em português, todas as palavras proparoxítonas são acentuadas. Isso significa que, independentemente de sua terminação ou do contexto, essas palavras sempre recebem o acento gráfico. Exemplos de palavras proparoxítonas Regras gerais sobre as proparoxítonas Diferença com outras palavras As palavras proparoxítonas têm uma característica única, pois, independente de sua terminação, sempre recebem o acento, o que as torna fáceis de identificar.
PALAVRAS PAROXÍTONAS

PALAVRAS PAROXÍTONAS As palavras paroxítonas são aquelas em que a penúltima sílaba é a tônica, ou seja, a sílaba pronunciada com maior intensidade. Ao contrário das palavras oxítonas (onde a tônica é a última sílaba) e das proparoxítonas (onde a tônica é a antepenúltima), as palavras paroxítonas têm a acentuação na penúltima sílaba. Regras de acentuação das palavras paroxítonas As palavras paroxítonas são acentuadas quando terminam em: Exemplos Exemplos de palavras paroxítonas não acentuadas Importante Diferença com as outras palavras
OXÍTONAS

PALAVRAS OXÍTONAS As palavras oxítonas são aquelas em que a última sílaba é a tônica, ou seja, a sílaba que se pronuncia com maior intensidade. Em português, as palavras oxítonas seguem uma regra específica para a acentuação. Regras de acentuação das palavras oxítonas As palavras oxítonas são acentuadas quando terminam em: Exemplos de palavras oxítonas acentuadas Exemplos de palavras oxítonas não acentuadas Acentuação nas oxítonas com “i” e “u” Diferença com outras palavras Em resumo, as palavras oxítonas são acentuadas quando terminam em -a(s), -e(s), -o(s), -em, -ens, com exemplos claros como café, também, pavão, entre outros.
DEFINIÇÃO DE CRASE

A palavra crase é de origem grega e significa “fusão”, “mistura”. Na língua portuguesa, é o nome que se dá à “junção” de duas vogais idênticas. É de grande importância a crase da preposição “a” com o artigo feminino “a” (s), com o pronome demonstrativo “a” (s), com o “a” inicial dos pronomes aquele (s), aquela (s), aquilo e com o “a” do relativo a qual (as quais). Na escrita, utilizamos o acento grave ( ` ) para indicar a crase. O uso apropriado do acento grave, depende da compreensão da fusão das duas vogais. É fundamental também, para o entendimento da crase, dominar a regência dos verbos e nomes que exigem a preposição “a”. Aprender a usar a crase, portanto, consiste em aprender a verificar a ocorrência simultânea de uma preposição e um artigo ou pronome. Observe: Vou a a igreja.Vou à igreja. No exemplo acima, temos a ocorrência da preposição “a”, exigida pelo verbo ir (ir a algum lugar) e a ocorrência do artigo “a” que está determinando o substantivo feminino igreja. Quando ocorre esse encontro das duas vogais e elas se unem, a união delas é indicada pelo acento grave. Observe os outros exemplos: Conheço a aluna.Refiro-me à aluna. No primeiro exemplo, o verbo é transitivo direto (conhecer algo ou alguém), logo não exige preposição e a crase não pode ocorrer. No segundo exemplo, o verbo é transitivo indireto (referir-se a algo ou a alguém) e exige a preposição “a”. Portanto, a crase é possível, desde que o termo seguinte seja feminino e admita o artigo feminino “a” ou um dos pronomes já especificados. Há duas maneiras de verificar a existência de um artigo feminino “a” (s) ou de um pronome demonstrativo “a” (s) após uma preposição “a”: 1- Colocar um termo masculino no lugar do termo feminino que se está em dúvida. Se surgir a forma ao, ocorrerá crase antes do termo feminino. Veja os exemplos: Conheço “a” aluna. / Conheço o aluno.Refiro-me ao aluno. / Refiro-me à aluna. 2- Trocar o termo regente acompanhado da preposição a por outro acompanhado de uma preposição diferente (para, em, de, por, sob, sobre). Se essas preposições não se contraírem com o artigo, ou seja, se não surgirem novas formas (na (s), da (s), pela (s),…), não haverá crase. Veja os exemplos: – Penso na aluna.– Apaixonei-me pela aluna.– Começou a brigar. – Cansou de brigar.– Insiste em brigar.– Foi punido por brigar.– Optou por brigar.
Conjuntos
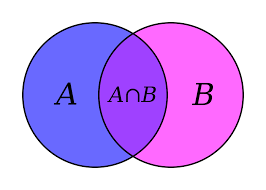
Conjunto é um conceito primitivo desenvolvido pelo matemático George Cantor. A partir dele se desenvolveu diversos outros estudos matemáticos. “A compreensão de conjuntos é a principal base para o estudo da álgebra e de conceitos de grande importância na Matemática, como funções e inequações. A notação que usamos para conjuntos é sempre uma letra maiúscula do nosso alfabeto (por exemplo, conjunto A ou conjunto B). Em se tratando da representação dos conjuntos, ela pode ser feita pelo diagrama de Venn, pela simples descrição das características dos seus elementos, pela enumeração dos elementos ou pela descrição das suas propriedades. Ao trabalhar com problemas que envolvem conjuntos, existem situações que exigem a realização de operações entre os conjuntos, sendo elas a união, a intersecção e a diferença. Vamos estudar tudo isso detalhadamente?” A teoria dos conjuntos é um ramo da matemática que estuda a coleção de objetos, chamados de elementos. Dessa forma, os elementos (que podem ser qualquer coisa: números, pessoas, frutas) são indicados por letra minúscula e definidos como um dos componentes do conjunto. Exemplo: o elemento “a” ou a pessoa “x”. Enquanto os elementos do conjunto são indicados por letra minúscula, os conjuntos, são representados por letras maiúsculas e, normalmente, com chaves { }. Além disso, os elementos são separados por vírgula ou ponto e vírgula, por exemplo: A = {a, e, i, o, u} Representação dos conjuntos Um conjunto pode ser representado de algumas maneiras. Cada uma delas têm vantagens e desvantagens, a depender do problema ou da situação em sejam usados. Diagrama de Euler-Venn No modelo de Diagrama de Euler-Venn (Diagrama de Venn), os conjuntos são representados graficamente. Imagens como círculos, elipses e retângulos formam uma área que “guarda” seus elementos. Esta figura plana fechada é chamada de diagrama. Os diagramas de Venn são úteis para representar conjuntos disjuntos (nenhum elemento em comum), assim como, conjuntos com elementos que se repetem. Representação de conjuntos na forma tabular A forma tabular utiliza os símbolos de chaves { } para representar conjuntos. Seus elementos devem estar separados por vírgulas. ExemplosA = {1, 3, 9, 12, 17} B = {João, Luíza, Fernando, Lívia} Representação de conjuntos por uma propriedade Um conjunto pode ser representado por uma regra que define uma característica comum em seus elementos. ExemplosA = {x / x é uma vogal} lemos: “O conjunto A é formado pelos elementos x, tal que x é uma vogal”. B = {x / x é múltiplo de 3} lemos: “O conjunto B é formado pelos elementos x, tal que x pertença aos números naturais e seja um múltiplo de 3.” Relação de Pertinência A relação de pertinência é um conceito muito importante na “Teoria dos Conjuntos”. Ela indica se o elemento pertence () ou não pertence () ao determinado conjunto, por exemplo: D = {w,x,y,z} Logo, (w pertence ao conjunto D) (j não pertence ao conjunto D) Isso significa que a pertinência é uma relação entre elementos e conjuntos. Relação de Inclusão A relação de inclusão aponta se tal conjunto está contido (C), não está contido (Ȼ) ou se um conjunto contém (Ɔ), algum subconjunto. Exemplo: A = {a,e,i,o,u}B = {a,e,i,o,u,m,n,o}C = {p,q,r,s,t} Logo, A C B (A está contido em B, ou seja, todos os elementos de A estão em B).C Ȼ B (C não está contido em B, pois os elementos dos conjuntos são diferentes).B Ɔ A (B contém A, pois todos elementos de A estão em B). Conjunto Vazio O conjunto vazio é o conjunto em que não há elementos; é representado por duas chaves { } ou pelo símbolo Ø. Note que o conjunto vazio está contido (C) em todos os conjuntos. União, Intersecção e diferença entre conjuntos As operações entre conjuntos são fundamentais para a solução de problemas. Cada operação possui suas características e regras. União de conjuntos A união, representada pela letra (U), corresponde a junção dos elementos de dois ou mais conjuntos, sem repetir elementos comuns. Exemplo A = {1, 2, 3, 4}B = {3, 4, 5, 6} Logo, A U B = {1, 2, 3, 4, 5, 6} Repare que os algarismos 3 e 4 foram representados uma única vez, mesmo estando presentes em A e B. Ao utilizar diagramas de Venn, a união é representada pelo preenchimento de toda imagem, não importando se são ou não disjuntos. Intersecção de conjuntos A intersecção, representada pelo símbolo (∩), corresponde aos elementos em comum de dois ou mais conjuntos. Assim, a intersecção é um novo conjunto, formado apenas pelos elementos que se repetem nos conjuntos iniciais. Exemplo C = {a, b, c, d, e}D = {d, e, f, g, h} Logo, C ∩ D = {d, e} Ao utilizar diagramas de Venn, a intersecção é representada pintando apenas a área onde os conjuntos estejam sobrepostos. Essa área “guarda” apenas os elementos repetidos. Diferença de conjuntos A diferença corresponde ao conjunto de elementos que estão no primeiro conjunto, e não aparecem no segundo, Exemplo A = {a, b, c, d, e} – B = {b, c, d, f, g} Logo, A – B = {a, e} Veja que a operação retirou os elementos comuns que existem em B. Na forma de diagrama, representamos como: Atenção!A subtração não é comutativa, ou seja, B – A não é igual à A – B. B – A = {f, g} Igualdade dos Conjuntos Na igualdade dos conjuntos, os elementos de dois conjuntos são idênticos, por exemplo, nos conjuntos A e B: A = {1,2,3,4,5}B = {3,5,4,1,2} Logo, A = B (A igual a B). Conjuntos Numéricos Os conjuntos numéricos são formados pelos:
Números
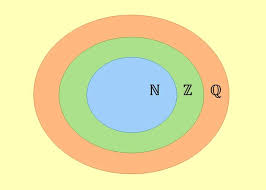
Número é uma entidade matemática fundamental e abstrata, utilizado para caracterizar a contagem, a ordenação, medição ou identificação. Os números possuem uma relação com elementos quaisquer, sejam reais ou não. Cada número descreve uma única característica para um dado elemento ou conjunto de elementos: Por exemplo, considere três maçãs. Há apenas um número que representa a quantidade destas frutas, o número 3. Ainda em relação ao exemplo anterior, considere pedir a um feirante três maçãs. O número caracteriza uma única quantidade possível e o feirante não terá dúvida alguma em lhe servir 3 maçãs. Assim, o número 3 caracteriza uma única quantidade existente possível, assim como, três unidades só podem ser caracterizadas por um único número existente, o próprio número 3. Números são, portanto, dispositivos que criam uma relação de “mão dupla” entre eles e as coisas do mundo (real ou imaginado). Na matemática essa relação recebe o nome de biunívoca. A representação dos números é feita por um numeral, expresso por sons, que podem ser representados por símbolos chamados de algarismos. Os algarismos correspondem à simbologia numérica, ou seja, os caracteres que identificam um número. Para Pitágoras, filósofo e matemático da Grécia Antiga, os números constituem o princípio de todas as coisas. História dos números A ideia de número foi construída ao longo da história. Desde a pré-história, a necessidade de contar e medir fez parte das atividades do homem primitivo. Ajuntamento de pedras, nós em cordas e riscos em superfícies foram algumas das formas utilizadas para registrar as quantidades no dia a dia. Os egípcios, por exemplo, por volta de 3500 a.C., criaram seu próprio sistema de contagem e escrita. A base da numeração egípcia era decimal e utilizava o princípio multiplicativo para desenvolver os números. Outros tipos de números são tão antigos quanto o dos egípcios, sendo criados para facilitar a tributação e a agricultura pelas civilizações. Os hindus inventaram um sistema de numeração, por volta do século VI, que foi difundido pela Europa Ocidental, provavelmente através dos árabes. Esse sistema indo-arábico são os algarismos que utilizamos hoje. Mohammed Ibu-Musa al-Khowarizmi, matemático árabe, descreveu em seu livro adição e subtração, conforme o cálculo hindu, a possibilidade de representar qualquer número utilizando apenas 10 símbolos, chamados de algarismos (1, 2, 3, 4, 5, 6, 7, 8, 9 e 0). De forma geral, os números surgiram e se desenvolveram impulsionados pelas necessidades sociais. Diversos sistemas de numeração foram criados em épocas e lugares diferentes. Cada sistema de numeração possuía suas próprias características e meios de representação. Com o tempo, o sistema indo-arábico prevaleceu e hoje, é usado pela maioria das pessoas ao redor do mundo. Com seu desenvolvimento, números com características semelhantes foram organizados e agrupados em conjuntos numéricos especiais.
Formação de Palavras

As palavras que compõem o léxico da língua são formadas principalmente por dois processos morfológicos: Palavras Primitivas e Derivadas Antes de mais nada, vale ressaltar dois conceitos importantes para o estudo de formação das palavras. Os vocábulos “primitivos” são as palavras que originam outras. Já as palavras “derivadas” são aquelas que surgem a partir das palavras primitivas Exemplos: Afixos Além do conceito de palavras primitivas e derivadas, temos os afixos. Eles são morfemas, ou seja, as menores partículas significativas da língua. Juntos a um radical, os afixos formam uma palavra, por exemplo, pedra (palavra primitiva) e pedreira (palavra derivada). Nesse exemplo, foi acrescentado o sufixo –eira. Os afixos são classificados de acordo com sua localização na palavra. Assim, os sufixos vêm depois do radical, por exemplo, folhagem e livraria. Já os prefixos são acrescentados antes do radical, por exemplo, desleal e ilegal. Além deles, há ainda os “infixos” que aparecem no meio da palavra, sendo representados por uma consoante ou vogal, por exemplo, cafeteria e cafezal. Radical e Prefixo Antes de analisar uma palavra e o processo pelo qual ela foi formada, faz-se necessário o conhecimento de seu radical e de seus prefixos. Segue abaixo alguns exemplos de radicais e prefixos gregos e latinos, ou seja, as línguas que mais influenciaram o léxico da língua portuguesa. Radicais Gregos Prefixos Gregos Radicais Latinos Prefixos Latinos Acro: alto, elevado acrobata a-, an-: negação Agri: campo ab- (abs-): afastamento Aero: ar anti-: ação contrária Ambi: ambos, duplicidade ad- (a-): proximidade, direção Antropo: homem dia-: movimento através Arbori: árvore ambi-: duplicidade Arcaio/ arqueo: antigo epi-: posição superior Avi: ave ante-: anterioridade Arquia: governo eu-: bem, bom Beli: guerra bem-: bom, êxito Hidro: água hiper-: excesso, posição superior Bi, bis: duas vezes bi-: dois Hipo: cavalo hipo-: deficiência Cultura: cultivar in-: negação Pseudo: falso meta-: mudança, transformação Curvi: curvo infra-: abaixo Psico: alma peri-: em torno de Ego: eu inter-: entre, posição intermediária Sofia: sabedoria pro-: anteriormente Equi: igual intra-: posição interior Processos de Derivação Os processos de derivação de palavras ocorrem de cinco maneiras, sempre com um radical e os afixos (sufixos e prefixos): Processos de Composição Os processos de composição de palavras envolvem mais de dois radicais de palavras, sendo classificadas em: Neologismo O neologismo é um processo de formação de palavras em que são criados novos termos para suprir alguma lacuna de significação. Podemos citar como exemplo a palavra “internetês”, que se refere à linguagem da internet. Hibridismo O hibridismo também é um processo de formação de palavras. Esses termos são formados com elementos de idiomas diferentes, por exemplo, “sociologia” (do latim, “sócio” e do grego “logia”).
QUÍMICA NO ENEM

QUÍMICA NO ENEM Os conteúdos de Química que mais caem no Enem são misturas e técnicas de separação; forças intermoleculares e polaridade; eletroquímica; estequiometria; termoquímica; Química orgânica; Química inorgânica; Química ambiental; e equilíbrio químico. Os conteúdos de Química no Enem são abordados dentro da área de Ciências da Natureza e suas Tecnologias, em conjunto com os conteúdos de Física e Biologia, em um conjunto de 45 questões de múltipla escolha. As questões do Enem são contextualizadas e multidisciplinares, sinalizando que o estudante encontrará questões que envolvem conceitos de diferentes disciplinas, quase sempre aplicados em situações reais.


