Lista Complementar
MATEMÁTICA BÁSICA

Conjuntos
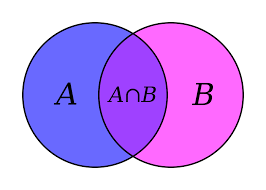
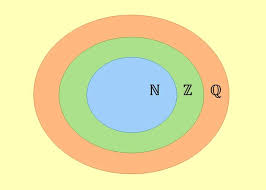
Conjunto é um conceito primitivo desenvolvido pelo matemático George Cantor. A partir dele se desenvolveu diversos outros estudos matemáticos. “A compreensão de conjuntos é a principal base para o estudo da álgebra e de conceitos de grande importância na Matemática, como funções e inequações. A notação que usamos para conjuntos é sempre uma letra maiúscula do nosso alfabeto (por exemplo, conjunto A ou conjunto B). Em se tratando da representação dos conjuntos, ela pode ser feita pelo diagrama de Venn, pela simples descrição das características dos seus elementos, pela enumeração dos elementos ou pela descrição das suas propriedades. Ao trabalhar com problemas que envolvem conjuntos, existem situações que exigem a realização de operações entre os conjuntos, sendo elas a união, a intersecção e a diferença. Vamos estudar tudo isso detalhadamente?” A teoria dos conjuntos é um ramo da matemática que estuda a coleção de objetos, chamados de elementos. Dessa forma, os elementos (que podem ser qualquer coisa: números, pessoas, frutas) são indicados por letra minúscula e definidos como um dos componentes do conjunto. Exemplo: o elemento “a” ou a pessoa “x”. Enquanto os elementos do conjunto são indicados por letra minúscula, os conjuntos, são representados por letras maiúsculas e, normalmente, com chaves { }. Além disso, os elementos são separados por vírgula ou ponto e vírgula, por exemplo: A = {a, e, i, o, u} Representação dos conjuntos Um conjunto pode ser representado de algumas maneiras. Cada uma delas têm vantagens e desvantagens, a depender do problema ou da situação em sejam usados. Diagrama de Euler-Venn No modelo de Diagrama de Euler-Venn (Diagrama de Venn), os conjuntos são representados graficamente. Imagens como círculos, elipses e retângulos formam uma área que “guarda” seus elementos. Esta figura plana fechada é chamada de diagrama. Os diagramas de Venn são úteis para representar conjuntos disjuntos (nenhum elemento em comum), assim como, conjuntos com elementos que se repetem. Representação de conjuntos na forma tabular A forma tabular utiliza os símbolos de chaves { } para representar conjuntos. Seus elementos devem estar separados por vírgulas. ExemplosA = {1, 3, 9, 12, 17} B = {João, Luíza, Fernando, Lívia} Representação de conjuntos por uma propriedade Um conjunto pode ser representado por uma regra que define uma característica comum em seus elementos. ExemplosA = {x / x é uma vogal} lemos: “O conjunto A é formado pelos elementos x, tal que x é uma vogal”. B = {x / x é múltiplo de 3} lemos: “O conjunto B é formado pelos elementos x, tal que x pertença aos números naturais e seja um múltiplo de 3.” Relação de Pertinência A relação de pertinência é um conceito muito importante na “Teoria dos Conjuntos”. Ela indica se o elemento pertence () ou não pertence () ao determinado conjunto, por exemplo: D = {w,x,y,z} Logo, (w pertence ao conjunto D) (j não pertence ao conjunto D) Isso significa que a pertinência é uma relação entre elementos e conjuntos. Relação de Inclusão A relação de inclusão aponta se tal conjunto está contido (C), não está contido (Ȼ) ou se um conjunto contém (Ɔ), algum subconjunto. Exemplo: A = {a,e,i,o,u}B = {a,e,i,o,u,m,n,o}C = {p,q,r,s,t} Logo, A C B (A está contido em B, ou seja, todos os elementos de A estão em B).C Ȼ B (C não está contido em B, pois os elementos dos conjuntos são diferentes).B Ɔ A (B contém A, pois todos elementos de A estão em B). Conjunto Vazio O conjunto vazio é o conjunto em que não há elementos; é representado por duas chaves { } ou pelo símbolo Ø. Note que o conjunto vazio está contido (C) em todos os conjuntos. União, Intersecção e diferença entre conjuntos As operações entre conjuntos são fundamentais para a solução de problemas. Cada operação possui suas características e regras. União de conjuntos A união, representada pela letra (U), corresponde a junção dos elementos de dois ou mais conjuntos, sem repetir elementos comuns. Exemplo A = {1, 2, 3, 4}B = {3, 4, 5, 6} Logo, A U B = {1, 2, 3, 4, 5, 6} Repare que os algarismos 3 e 4 foram representados uma única vez, mesmo estando presentes em A e B. Ao utilizar diagramas de Venn, a união é representada pelo preenchimento de toda imagem, não importando se são ou não disjuntos. Intersecção de conjuntos A intersecção, representada pelo símbolo (∩), corresponde aos elementos em comum de dois ou mais conjuntos. Assim, a intersecção é um novo conjunto, formado apenas pelos elementos que se repetem nos conjuntos iniciais. Exemplo C = {a, b, c, d, e}D = {d, e, f, g, h} Logo, C ∩ D = {d, e} Ao utilizar diagramas de Venn, a intersecção é representada pintando apenas a área onde os conjuntos estejam sobrepostos. Essa área “guarda” apenas os elementos repetidos. Diferença de conjuntos A diferença corresponde ao conjunto de elementos que estão no primeiro conjunto, e não aparecem no segundo, Exemplo A = {a, b, c, d, e} – B = {b, c, d, f, g} Logo, A – B = {a, e} Veja que a operação retirou os elementos comuns que existem em B. Na forma de diagrama, representamos como: Atenção!A subtração não é comutativa, ou seja, B – A não é igual à A – B. B – A = {f, g} Igualdade dos Conjuntos Na igualdade dos conjuntos, os elementos de dois conjuntos são idênticos, por exemplo, nos conjuntos A e B: A = {1,2,3,4,5}B = {3,5,4,1,2} Logo, A = B (A igual a B). Conjuntos Numéricos Os conjuntos numéricos são formados pelos:
Números
Número é uma entidade matemática fundamental e abstrata, utilizado para caracterizar a contagem, a ordenação, medição ou identificação. Os números possuem uma relação com elementos quaisquer, sejam reais ou não. Cada número descreve uma única característica para um dado elemento ou conjunto de elementos: Por exemplo, considere três maçãs. Há apenas um número que representa a quantidade destas frutas, o número 3. Ainda em relação ao exemplo anterior, considere pedir a um feirante três maçãs. O número caracteriza uma única quantidade possível e o feirante não terá dúvida alguma em lhe servir 3 maçãs. Assim, o número 3 caracteriza uma única quantidade existente possível, assim como, três unidades só podem ser caracterizadas por um único número existente, o próprio número 3. Números são, portanto, dispositivos que criam uma relação de “mão dupla” entre eles e as coisas do mundo (real ou imaginado). Na matemática essa relação recebe o nome de biunívoca. A representação dos números é feita por um numeral, expresso por sons, que podem ser representados por símbolos chamados de algarismos. Os algarismos correspondem à simbologia numérica, ou seja, os caracteres que identificam um número. Para Pitágoras, filósofo e matemático da Grécia Antiga, os números constituem o princípio de todas as coisas. História dos números A ideia de número foi construída ao longo da história. Desde a pré-história, a necessidade de contar e medir fez parte das atividades do homem primitivo. Ajuntamento de pedras, nós em cordas e riscos em superfícies foram algumas das formas utilizadas para registrar as quantidades no dia a dia. Os egípcios, por exemplo, por volta de 3500 a.C., criaram seu próprio sistema de contagem e escrita. A base da numeração egípcia era decimal e utilizava o princípio multiplicativo para desenvolver os números. Outros tipos de números são tão antigos quanto o dos egípcios, sendo criados para facilitar a tributação e a agricultura pelas civilizações. Os hindus inventaram um sistema de numeração, por volta do século VI, que foi difundido pela Europa Ocidental, provavelmente através dos árabes. Esse sistema indo-arábico são os algarismos que utilizamos hoje. Mohammed Ibu-Musa al-Khowarizmi, matemático árabe, descreveu em seu livro adição e subtração, conforme o cálculo hindu, a possibilidade de representar qualquer número utilizando apenas 10 símbolos, chamados de algarismos (1, 2, 3, 4, 5, 6, 7, 8, 9 e 0). De forma geral, os números surgiram e se desenvolveram impulsionados pelas necessidades sociais. Diversos sistemas de numeração foram criados em épocas e lugares diferentes. Cada sistema de numeração possuía suas próprias características e meios de representação. Com o tempo, o sistema indo-arábico prevaleceu e hoje, é usado pela maioria das pessoas ao redor do mundo. Com seu desenvolvimento, números com características semelhantes foram organizados e agrupados em conjuntos numéricos especiais.
Matemática no Enem

A prova de matemática do Enem (Matemática e suas tecnologias) é a única prova que apresenta uma disciplina isolada, o que a torna o maior peso individual do concurso. As questões da prova são objetivas, com 5 alternativas de resposta, apresentam enunciados contextualizados e cobram um conhecimento global do aluno. Conteúdos que mais caem na prova de matemática Veja os conteúdos de Matemática mais cobrados no Enem dos últimos 9 anos: 1. Grandezas proporcionais Grandezas proporcionais, que engloba os conteúdos de razão e proporção, regra de três, porcentagem e escalas, é o que mais aparece nas questões de Matemática. O fato deste conteúdo ser aplicado nas mais variadas situações do cotidiano, faz com que seja muito explorado no Enem. Esse tipo de cálculo pode aparecer em questões que cobrem diretamente a relação entre grandezas ou em problemas onde este cálculo é usado em uma das etapas da sua resolução. Exemplo (Enem – 2017) Às 17 h 15 min começa uma forte chuva, que cai com intensidade constante. Uma piscina em forma de um paralelepípedo retângulo, que se encontrava inicialmente vazia, começa a acumular a água da chuva e, às 18 horas, o nível da água em seu interior alcança 20 cm de altura. Nesse instante, é aberto o registro que libera o escoamento da água por um ralo localizado no fundo dessa piscina, cuja vazão é constante. Às 18 h 40 min a chuva cessa e, nesse exato instante, o nível da água na piscina baixou para 15 cm. O instante em que a água dessa piscina terminar de escoar completamente está compreendido entre a) 19 h 30 min e 20 h 10 minb) 19 h 20 min e 19 h 30 minc) 19 h 10 min e 19 h 20 mind) 19 h e 19 h 10 mine) 18 h 40 min e 19 h


